Simulaciones de elementos infinitos espectrales de anomalías magnéticas
Se implementa un método de elemento infinito espectral para calcular anomalías magnéticas resolviendo una forma discretizada de la ecuación de Poisson Laplace.
El método de elemento infinito espectral combina el método altamente preciso del elemento espectral con el método de elemento infinito, que reproduce un dominio ilimitado de manera precisa y eficiente.
Esta combinación es posible mediante el acoplamiento de la cuadratura de Gauss-Legendre-Lobatto en elementos espectrales con la cuadratura de Gauss-Radau en elementos infinitos a lo largo de direcciones infinitas.
El método tiene dos ventajas distintivas sobre los métodos tradicionales. Primero, la discretización de orden superior produce con precisión heterogeneidades magnetizadas complejas.
Segundo, dado que el tiempo de cálculo es independiente del número de puntos de observación, el método es eficiente para modelos muy grandes.
En este artículo se ilustra la precisión y la eficiencia del método comparando anomalías magnéticas calculadas para varias heterogeneidades magnetizadas con las correspondientes soluciones analíticas y computacionales de uso común.
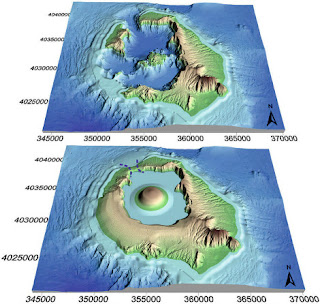
Se concluye con un ejemplo práctico que involucra un complejo modelo 3D de una mina de mineral.
Hom Nath Gharti, Jeroen Tromp; Spectral-infinite-element simulations of magnetic anomalies, Geophysical Journal International, https://doi.org/10.1093/gji/ggz107
El método de elemento infinito espectral combina el método altamente preciso del elemento espectral con el método de elemento infinito, que reproduce un dominio ilimitado de manera precisa y eficiente.
Esta combinación es posible mediante el acoplamiento de la cuadratura de Gauss-Legendre-Lobatto en elementos espectrales con la cuadratura de Gauss-Radau en elementos infinitos a lo largo de direcciones infinitas.
El método tiene dos ventajas distintivas sobre los métodos tradicionales. Primero, la discretización de orden superior produce con precisión heterogeneidades magnetizadas complejas.
Segundo, dado que el tiempo de cálculo es independiente del número de puntos de observación, el método es eficiente para modelos muy grandes.
En este artículo se ilustra la precisión y la eficiencia del método comparando anomalías magnéticas calculadas para varias heterogeneidades magnetizadas con las correspondientes soluciones analíticas y computacionales de uso común.
Se concluye con un ejemplo práctico que involucra un complejo modelo 3D de una mina de mineral.
Hom Nath Gharti, Jeroen Tromp; Spectral-infinite-element simulations of magnetic anomalies, Geophysical Journal International, https://doi.org/10.1093/gji/ggz107