Presión de fluido y deformación de rocas usando observaciones de velocidad sísmica
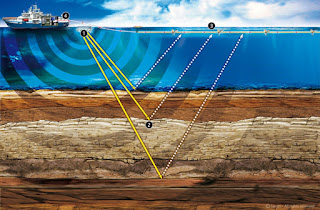
La presión del fluido dentro de la corteza terrestre es un factor clave para desencadenar la sismicidad natural e inducida por el hombre. Medir la evolución de la presión del fluido sería altamente beneficioso para comprender los mecanismos de conducción subyacentes y respaldar la evaluación de peligros sísmicos.
En este artículo se muestra que las velocidades sísmicas monitoreadas en el rango de 20 m responden directamente a los cambios en la presión del fluido.
Los datos muestran que la deformación volumétrica resultante de los cambios efectivos de esfuerzos se detecta por la velocidad sísmica, mientras que la dislocación por cizalladura no lo es.
Se puede calibrar la evolución de la velocidad sísmica contra la presión del fluido y la deformación con mediciones in situ durante un experimento de inyección de fluido a una escala de decímetros en una roca cristalina.
Por lo tanto, nuestros tomogramas sísmicos 4D permiten el seguimiento de la presión del fluido y la evolución de la deformación.
Los hallazgos demuestran un gran potencial para monitorear las variaciones transitorias de la presión del fluido y los cambios de esfuerzos en sitios de campo bien instrumentados y podrían extenderse para monitorear las estimulaciones hidráulicas en depósitos profundos.
Método
Medidas de laboratorio de módulos elásticos
Tres muestras cilíndricas se cargaron uniaxialmente para analizar la respuesta a la deformación utilizando un modelo de material de isotropía transversal. Este modelo define un plano de isotropía, que se asume como coincidente con el plano de foliación, donde la respuesta de deformación es isotrópica y se describe mediante el módulo de Young en el plano y la relación de Poisson E,ν. En la dirección perpendicular al plano de isotropía, se definen el módulo de Young transversal E' y la relación de Poisson ν'. Las constantes elásticas estáticas tangentes se midieron utilizando la metodología de Nejati (2018) a un nivel de esfuerzo de 11 MPa. Además, se emplearon mediciones ultrasónicas para obtener la dependencia direccional de la velocidad de la onda P, a partir de la cual se calcularon las constantes elásticas dinámicas sin tensión de confinamiento (Nejati, 2018). Combinando estos datos con las velocidades medidas en campo, también se determinó la dependencia del esfuerzo de los módulos dinámicos.
Doetsch, J., Gischig, V. S., Villiger, L., Krietsch, H., Nejati, M., Amann, F., et al (2018). Subsurface Fluid Pressure and Rock Deformation Monitoring using Seismic Velocity Observations. Geophysical Research Letters. https://doi.org/10.1029/2018GL079009
 |
| El modelo se basa en más de 10 000 tiempos de viaje desde un pozo de perforación hasta los receptores sísmicos. Este modelo se utiliza para calcular las trayectorias y sensibilidades para la inversión de lapso de tiempo. |
En este artículo se muestra que las velocidades sísmicas monitoreadas en el rango de 20 m responden directamente a los cambios en la presión del fluido.
Los datos muestran que la deformación volumétrica resultante de los cambios efectivos de esfuerzos se detecta por la velocidad sísmica, mientras que la dislocación por cizalladura no lo es.
Se puede calibrar la evolución de la velocidad sísmica contra la presión del fluido y la deformación con mediciones in situ durante un experimento de inyección de fluido a una escala de decímetros en una roca cristalina.
 |
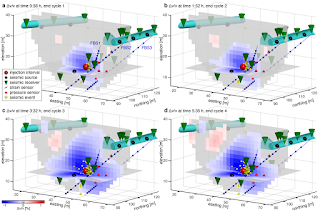| a-d muestra el cambio de velocidad relativa con respecto a la línea base de pre-estimulación al final de los cuatro ciclos de inyección. |
Por lo tanto, nuestros tomogramas sísmicos 4D permiten el seguimiento de la presión del fluido y la evolución de la deformación.
Los hallazgos demuestran un gran potencial para monitorear las variaciones transitorias de la presión del fluido y los cambios de esfuerzos en sitios de campo bien instrumentados y podrían extenderse para monitorear las estimulaciones hidráulicas en depósitos profundos.
 |
| La mayoría de los eventos sísmicos (círculos amarillos) se concentran dentro de los 5 m y al este del punto de inyección. |
Método
Medidas de laboratorio de módulos elásticos
Tres muestras cilíndricas se cargaron uniaxialmente para analizar la respuesta a la deformación utilizando un modelo de material de isotropía transversal. Este modelo define un plano de isotropía, que se asume como coincidente con el plano de foliación, donde la respuesta de deformación es isotrópica y se describe mediante el módulo de Young en el plano y la relación de Poisson E,ν. En la dirección perpendicular al plano de isotropía, se definen el módulo de Young transversal E' y la relación de Poisson ν'. Las constantes elásticas estáticas tangentes se midieron utilizando la metodología de Nejati (2018) a un nivel de esfuerzo de 11 MPa. Además, se emplearon mediciones ultrasónicas para obtener la dependencia direccional de la velocidad de la onda P, a partir de la cual se calcularon las constantes elásticas dinámicas sin tensión de confinamiento (Nejati, 2018). Combinando estos datos con las velocidades medidas en campo, también se determinó la dependencia del esfuerzo de los módulos dinámicos.
Doetsch, J., Gischig, V. S., Villiger, L., Krietsch, H., Nejati, M., Amann, F., et al (2018). Subsurface Fluid Pressure and Rock Deformation Monitoring using Seismic Velocity Observations. Geophysical Research Letters. https://doi.org/10.1029/2018GL079009
