Tomografía de tiempo de viaje dependiente de la frecuencia para datos de refracción sísmica cerca de la superficie.
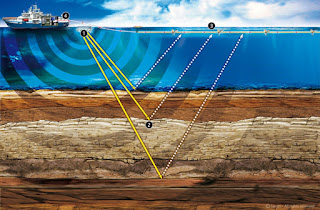
La tomografía de tiempo de viaje es el método principal por el cual la velocidad sísmica de la Tierra se determina a todas las escalas, desde la cerca de la superficie (<100 m) hasta el núcleo. Comúnmente, la tomografía de tiempo de viaje utiliza la teoría de rayos, una aproximación de frecuencia-infinita de la propagación de onda.
Una teoría desarrollada en la sismología a nivel mundial para considerar la naturaleza de la frecuencia-finita de los datos sísmicos, conocida como tomografía de tiempo de viaje de frecuencia-finita (FFTT), puede teóricamente, proporcionar una estimación más precisa de la velocidad. Sin embargo, la teoría FFTT, no es aplicable generalmente a datos cerca de la superficie ya que no existe un modelo de velocidad de referencia conocido con anticipación que sea capaz de producir formas de onda sintéticas que sean lo suficientemente cercanas a los sismogramas registrados para obtener un tiempo de retardo confiable. Además, por lo general no existe un modelo de referencia para el que el modelo de velocidad desconocido, represente una pequeña perturbación (lineal) a partir del modelo de referencia.
Este artículo presenta una forma dependiente de la frecuencia de tomografía de tiempo de viaje no lineal, diseñada específicamente, para datos sísmicos cerca de la superficie en la que un modelo de inicio, se aproxima iterativamente con trayectorias de viaje recalculadas en cada iteración, y se utiliza el cálculo dependiente de la frecuencia del tiempo de viaje total, al contrario del tiempo de retardo. La tomografía de tiempo de viaje dependiente de la frecuencia (FDTT) implica dos modificaciones a la tomografía de tiempo de viaje convencional: (1) el cálculo de tiempos de viaje dependientes de la frecuencia utilizando el suavizado de longitud de onda dependiente de la velocidad (WDVS) y (2) los kernels correspondientes que surgen del uso de WDVS.
Los resultados muestran que la modificación anterior es esencial para lograr beneficios significativos de FDTT, mientras que la última es opcional ya que resultados similares se pueden alcanzar utilizando kernels de frecuencia infinita. Las grandes longitudes de onda sísmica, relativas a las longitudes de trayectoria totales, y al tamaño de las heterogeneidades del subsuelo de datos cerca de la superficie típicos, quiere decir que las mejoras son significativas con respecto a la tomografía de la teoría de rayos.
Los beneficios de FDTT se demuestran utilizando técnicas de estructura mínima de regularización convencionales para abordar el problema del modelo de no unicidad. Para datos sintéticos, los modelos estimados de FDTT demuestran ser más precisos que los modelos correspondientes de derivados frecuencia-infinita.Las aplicaciones de FDTT tanto en 2-D y en 3-D a datos reales de un estudio cerca de la superficie, producen modelos estimados que contienen más estructura que los correspondientes a los modelos derivados de frecuencia-infinita.
Las aplicaciones de FDTT sin regularización demuestran el potencial de los kernels de sensibilidad derivada de WDVS para proporcionar un suavizado natural del modelo de velocidad y de ese modo permitir que los datos por si mismos determinen la estructura del modelo final.
Geophysical Journal Int.
doi: 10.1093/gji/ggw269